Transport & Other Lagrangian Transforms

Imaging and data science lab


Latest papers: (see below for more)

    • (07/22) End-to-end Signal Classification in Signed Cumulative Distribution Space, Paper, Software: PyTransKit .
    • Illumination invariant face recognition using optimal transport Preprint , code , PyTransKit .
    • The signed cumulative distribution transform (SCDT) for signal analysis and classification, SIAM Foundation of data science, 2022. Preprint , Software: PyTransKit .
    • R-CDT subspace models for image classification, JMIV, 2021 paper , python code , Matlab code
    • Partitioning signal classes using transport transforms, SaSiDa, 2021, preprint
    • Pre-symptomatic early detection of osteoarthritis from knee MRIs. PNAS, 2020.
    • Wasserstein embedding for graph learning, 2020, paper
    • Parametric signal estimation using the cumulative distribution transform, IEEE Transactions on Signal Processing 2020, paper

Software: (see below for more)

    • Pytranskit: Python Transport Signal/Image Processing Toolkit

Motivation

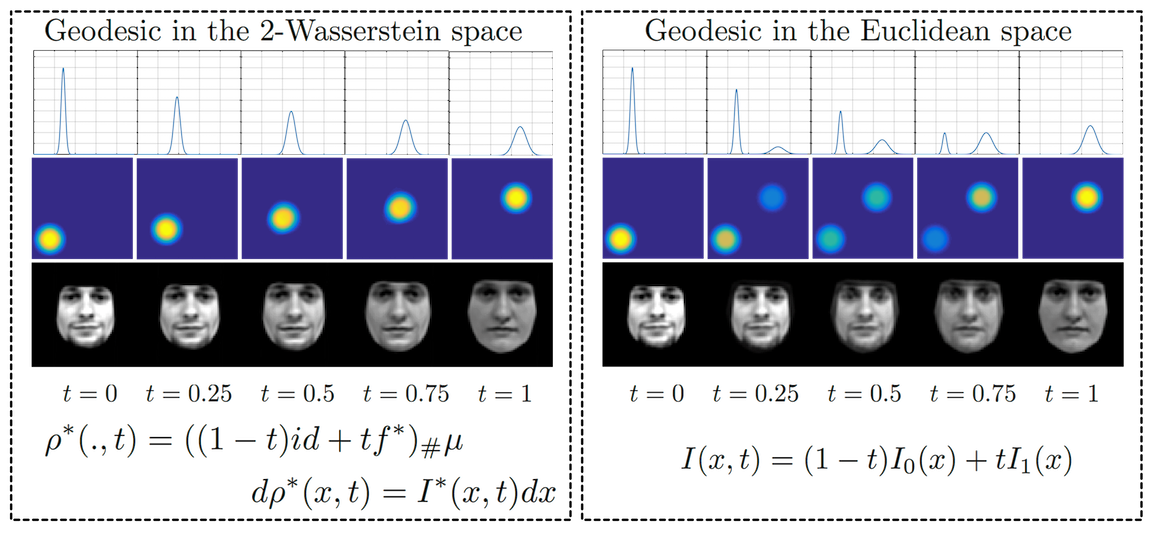
Most mathematical tools for processing signals and images rely on the manipulation of signal/pixel intensities at `fixed' positions on a pixel grid. The success of modern algorithms for data analysis such as registration/tracking, dynamic time-warping, neural networks, etc., however, has taught us that both 1) nonlinearity, and 2) modeling the location of pixel intensities are essential concepts to keep in mind when solving modern problems related to estimation and classification. Our goal is thus to establish a mathematical signal representation method based on the idea of matching signals & images by pixel displacement operations that are physically related to the concept of transport phenomena. The figure shown on the left gives examples of matching signals in 1D using the Transport/Wasserstein geometry, versus matching signals with the traditional Euclidean/Lp-based methods. It can be seen the Lagrangian framework enables signal intensities to be carried/transported through the signal domain, thus enabling more meaningful comparisons.

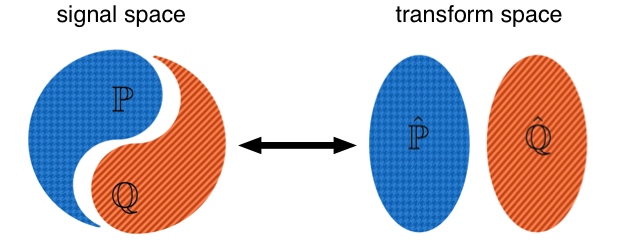
There are multiple benefits offered by representing signals with the Lagrangian framework including the ability to model signal texture and shapes simultaneously, obtaining more parsimonious representations, as well as simplifying the solution to pattern recognition problems (e.g. classification). For example, the Lagrangian signal representation framework can be shown to make signal classes (e.g. classifying handwritten digits, benign vs malignant cancer cells, etc.) more convex and thus more easily (e.g. linearly) separable.

In addition to theory, our project also aims to test these idea in diverse fields including machine learning, optics, computer vision and biomedical imaging. Specific applications include: able to distinguish between benign and malignant tumors in medical images, learning models (e.g., dictionaries) for solving inverse problems, identifying people from images of faces, voice profiles, or fingerprints; and many others.

Publications

Overviews

  • S Kolouri, SR Park, M Thorpe, D Slepcev, GK Rohde, Optimal mass transport for signal processing and machine learning, IEEE Signal Processing Magazine, 34(4), pp 43-59, 2017. paper , code
  • S Kolouri, SR Park, M Thorpe, D Slepčev, GK Rohde, Transport-based analysis, modeling, and learning from signal and data distributions, Arxiv preprint , 2016.

Signal & image representation/transforms:

  • The signed cumulative distribution transform (SCDT) for signal analysis and classification, SIAM Foundation of data science, 2022. Preprint , Software: PyTransKit .
  • Partitioning signal classes using transport transforms, SaSiDa, 2021, preprint
  • SR Park, S Kolouri, S Kundu, GK Rohde, The Cumulative Distribution Transform and Linear Pattern Classification, Applied and Computational Harmonic Anaysis, 2018. preprint , journal , Matlab software , iPython notebook example , github tutorial
  • M Thorpe, SR Park, S Kolouri, GK Rohde, D Slepcev, A Transportation Lp Distance for Signal Analysis, Journal of Mathematical Imaging and Vision, 2017. paper , code (warning ~2GB)
  • S Kolouri, SR Park, GK Rohde, The Radon cumulative distribution transform and its application to image classification, IEEE Transactions on Image Processing, 25(2), pp 920-934, 2016. Preprint available at arXiv:1511.03206. link , Matlab software , iPython notebook example
  • S Kolouri, AB Tosun, JA Ozolek, GK Rohde, A Continuous Linear Optimal Transport Approach for Pattern Analysis in Image Datasets, Pattern Recognition, 2016. preprint , journal site .
  • W Wang, D Slepcev, JA Ozolek, S Basu, GK Rohde, A linear optimal transportation framework for quantifying and visualizing variations in sets of images. International Journal of Computer Vision, vol. 101(2), pp. 254-269, 2013. Journal site , pdf .

Machine learning:

  • Rubaiyat et al, End-to-end Signal Classification in Signed Cumulative Distribution Space, 2022, Paper, Software: PyTransKit .
  • Shifat-E-Rabbi et al, Invariance encoding in sliced-Wasserstein space for image classification with limited training data, preprint , 2022
  • Shifat-E-Rabbi et al, R-CDT subspace models for image classification, JMIV, 2021 paper , python code , Matlab code , PyTransKit .
  • S Kolouri, N Nadarializadeh, GK Rohde, H Hoffman, Wasserstein embedding for graph learning, 2020, paper
  • S Kolouri, K Nadjahi, U Simsekli, R Badeau, GK Rohde Generalized sliced Wasserstein distances: NeurIPS 2019 paper
  • S Kolouri, CE Martin, GK Rohde, Sliced-Wasserstein Autoencoder, ICLR 2019. preprint , code
  • S Kolouri, GK Rohde, H Hoffman, Sliced Wasserstein Distance for Learning Gaussian Mixture Models, CVPR 2018. paper , code
  • S Kolouri, Y Zou, GK Rohde, Sliced Wasserstein Kernels for Probability Distributions, arXiv:1511.03198. CVPR 2016. link , software

Applications

  • Zhuang et al, Illumination invariant face recognition using optimal transport Preprint , code , PyTransKit .
  • Pre-symptomatic early detection of osteoarthritis from knee MRIs. In press, PNAS, 2020. paper
  • Rubaiyat, Hallam, Nichols, Hutchinson, Li, Rohde, Parametric signal estimation using the cumulative distribution transform, IEEE Transactions on Signal Processing 2020, paper
  • JM Nichols, MN Hutchinson, N Menkart, GA Cranch, GK Rohde, Time Delay Estimation Via Wasserstein Distance Minimization, IEEE Signal Processing Letters, 2019, paper
  • JM Nichols, TH Emerson, L Cattell, S Park, A Kanaev, F Bucholtz, A Watnik, T Doster, and GK Rohde, Transport-based model for turbulence-corrupted imagery, Applied Optics, 57(16) pp. 4524-4536, 2018. paper
  • SR Park, L Cattell, JM Nichols, A Watnik, T Doster, GK Rohde, De-multiplexing vortex modes in optical communications using transport-based pattern recognition. Optics express 26(4), pp 4004-4022, 2018. paper
  • S Kundu, S Kolouri, KI Erickson, AF Kramer, E McAuley, GK Rohde, Discovery and visualization of structural biomarkers from MRI using transport-based morphometry, Neuroimage 2018, paper
  • L Cattell, CH Meyer, FH Epstein, GK Rohde, Reconstructing High-Resolution Cardiac MR Movies from Under-Sampled Frames, Asilomar conference on signals, systems, and computers, 2017. paper
  • S Kolouri, GK Rohde, Transport-based single frame super resolution of very low resolution face images. IEEE CVPR 2015, pp 4876-4884. pdf 
  • AB Tosun, A Yergiev, S Kolouri, J Silverman, GK Rohde, Detection of malignant mesothelioma using nuclear structure of mesothelial cells in effusion cytology specimens, Cytometry A, 87(4), 326-333, 2015. pdf
  • S Kolouri, S Basu, GK Rohde, Learning and visualizing statistical relationships betwen protein distributions from microscopy images. IEEE ISBI 2014, pp 381-384. paper
  • JA Ozolek, AB Tosun, W Wang, C Chen, S Kolouri, S Basu, H Huang, GK Rohde. Accurate diagnosis of thyroid follicular lesions from nuclear morphology using supervised learning. Medical Image Analysis. 18(5), 772-780, 2014. link
  • S Basu, S Kolouri, GK Rohde, Detecting and visualizing cell phenotype differences from microscopy images using transport-based morphometry. PNAS 111 (9), 3448-3453, 2014. pdf , publisher , software
  • W Wang, JA Ozolek, D Slepcev, AB Lee, C Chen, GK Rohde, An optimal transportation approach for nuclear structure-based pathology, IEEE Transactions on Medical Imaging, 30, pp. 621-631, 2011. (pdf)

Presentations & Classes & Tutorials

Codes

  • PyTransKit, Transport and other Lagrangian transforms python toolkit code
  • R-CDT subspaces for image classification: python code
  • CDT iPython notebook example: iPynb paper
  • Radon-CDT iPython notebook example: iPynb paper
  • Tutorial code: Zip Directory paper
  • DiscreteLOT: Matlab software for computing a particle-based linear optimal transport embedding of images of cells, as well as applying the transport-based morphometry pipeline described in Basu et al, PNAS 2014. To run the software, download and run the script "Main_LOT_Particle.m". PDF Software
  • 1D CDT: Python software for computing the 1D cummulative distribution transform (CDT), as described in Park et al arXiv:1507.05936, 2015. To run the software, download and run the iPythonNoteBook script provided. If desired, a Matlab software for 1D CDT is also provided. paper Python MATLAB
  • 2D Continuous LOT: Matlab software for computing the 2D continuous linear optimal transport (LOT) transform as described in Kolouri et al, Pattern Recognition 2015 (in press). To run the software, download and run the script "main.m". Preprint Software
  • 2D Radon-CDT: Matlab software for computing the 2D Radon cumulative distribution transform as described in Kolouri et al, IEEE TIP 2016. To run the software, download and run the script "main.m". Preprint Software